Skip to content

07

记录以下期末考试之前的复习内容。

人工智能基础

Quote

"In the field of artificial intelligence, while mathematics plays a significant role, it is not necessarily the most crucial aspect. Instead, the underlying philosophy and methodology behind mathematics holds greater importance." M.T.Dickens (2024)

符号推演算法

FOIL 算法

FOIL，全程为 First Order Inductive Learner。

具体步骤：

  1. 给出一个知识图谱（即背景知识样例集合），里面有各种关系，也就是一阶量词的具体形式
  2. 确定个体词的个数 （本例中就是 \(x,y,z\) 三个）
  3. 确定使用量词的个数 （本例中就是两个：$ \dots \larr _1_ \land _2_$）
  4. 确定希望推演的目标关系 （本例中是 \(Father(x,y)\)），以及对应的目标谓词训练样例集合。

举例：

graph LR
    1((Mary))
    2((David))
    3((Ann))
    4((Mike))
    1 <--Couple--> 2
    1 --Mother--> 3
    3 <--Sibling--> 4
    2 --Father--> 4
    1 --Mother--> 4
背景知识样例集合 目标谓词训练样例集合
Mother(Mary, Ann) Father(David, Mike)
Mother(Mary, Mike) ~Father(Mary, Ann)
Couple(David, Mary) ~Father(Mary, Mike)
Sibling(Ann, Mike) ~Father(Mary, David)
~Father(Ann, Mike)

FOIL 信息增益公式： $$ FOIL_GAIN = \widehat {m_+} (\log \frac {\widehat {m_+}} {\widehat {m_+} + \widehat {m_-}} - \log \frac { {m_+}} { {m_+} + {m_-}}) $$ 如何计算 \(\widehat {m_+}\) 和 \(\widehat {m_-}\)：

具体地，我们将所有目标集合中的样例（不论正例、反例）列出来，令 \(x, y\) 分别等于对应的值。此时，如果我们能够找到剩余变量（e.g. 对于 Father(x,y) \(\larr\) Mother(z,y)，即 \(z\)）的一种赋值，使得“箭头右边为真”，则该样例计入 \(\widehat {m_+}\) 或 \(\widehat {m_-}\)。

\(\widehat {m_+}\) \(\widehat {m_-}\) \(FOIL\_GAIN\)
Father(x,y) [基准] 1 4 -
Father(x,y) \(\larr\) Mother(z,y) 1 3 0.322
Father(x,y) \(\larr\) Sibling(z,y) 1 2 0.737
Father(x,y) \(\larr\) Couple(x,z) 1 0 2.322
Father(x,y) \(\larr\) Couple(z,x) 0 2 NaN

举例：Father(x,y) \(\larr\) Sibling(z,y)

令 \(x = David, y = Mike\)，则存在 \(Sibling(Ann, Mike)\)，因此计入 \(\widehat {m_+}\)

令 \(x = Mary, y = Ann\)，则不存在，因此不计入

令 \(x = Mary, y = Mike\)，则存在 \(Sibling(Ann, Mike)\)，因此计入 \(\widehat {m_-}\)

令 \(x = Mary, y = David\)，则不存在，因此不计入

令 \(x = Ann, y = Mike\)，则存在 \(Sibling(Ann, Mike)\)，因此计入 \(\widehat {m_-}\)

从而 \(\widehat {m_+} = 1\)，\(\widehat {m_-} = 2\)，又因为 \({m_+} = 1, {m_-} = 4\) $$ FOIL_GAIN = 1 (\log \frac {1} {1 + 2} - \log \frac { 1} { 1+ 4}) = \log \frac 5 3 = 0.7369\dots $$

算法时间复杂度

假设背景知识样例集合大小为 \(n_1\)，目标谓词训练样例集合为 \(n_2\)，个体词的个数为 \(c_1\)，使用量词的个数为 \(c_2\)，量词总数为 \(d_1\)，量词变量数为 \(d_2\)，则： 推理第 \(k\) 个量词的时候，需要的时间为： \(\binom {c_1} {d_2} * d_1 * n_2 * (\mathrm{time \ to\ find\ a\ satisfication\ or\ prove\ no\ satifsication\ for\ a\ single\ pair\ of}(x_1, x_2, \cdots, x_{d_2}))\)

  • 括号里的时间我懒得算了

总共时间为所有上述时间之和。

因此，在 \(c_1, d_1\) 较大的时候，推理难度是很大的。

概率图模型

贝叶斯网络

顾名思义，就是使用贝叶斯条件概率公式，来计算出联合概率分布。

网络性质

对于每一个节点，其包含

  • 一个事件
  • 一些箭头，指向父节点
  • 说明该节点的事件的概率依赖于父节点事件
  • 一个概率表，标记出该节点事件在所有父节点事件的下的条件概率
  • 假设一共有 \(k\) 个父节点，由于父节点事件就是布尔变量，故概率表大小为 \(\mathcal O(2^k)\)

另外，我们采用马尔可夫性假设：不相连的节点，条件概率中可以删去。

  • e.g 对于图
graph TD
  A --> B
  A --> C
  B --> D
  C --> D

\(\Pr(A, B, C, D) = \Pr(A | B, C, D) \Pr(B | C, D) \Pr(C | D) \Pr(D) = \Pr(A | B, C) \Pr(B | D) \Pr(C | D) \Pr(D)\)

从而，我们可以使用贝叶斯公式，计算出任何事件的条件/边缘/联合概率等等。

马尔可夫网络

也是开局一张图。不同的是，节点和节点之间，不再是纯粹条件概率的关系，而是加入了一阶谓词。

从概率统计角度来看，马尔可夫逻辑网络不仅简洁明了描述了马尔可夫网(Markov networks，简称MNs)中所存在信息之间关联，还因在马尔可夫网络中引入谓词逻辑融入了结构化知识；

从一阶谓词逻辑角度来看，马尔可夫逻辑网在一阶谓词逻辑中添加了不确定性而对严格推理进行了松绑，更好反映了客观世界的复杂性

公式

给定一个由若干规则构成的集合，集合中每条推理规则赋予一定权重，则可如下计算某个断言 \(x\) 成立的概率： $$ \Pr(X = x) = \frac 1 Z \exp(\sum_i w_i n_i(x)) = \frac 1 Z \prod_i \phi_i(x_{{i}})^{n_i(x)} $$ 其中，其中 \(n_i(x)\) 是在推导 \(x\) 中所涉及第 \(i\) 条规则的逻辑取值（为 1 或 0）、\(w_i\) 是该规则对应的 权重（事情越重要，权重越高），\(Z\) 是一个固定的归一化常量，可由下式计算： $$ Z = \sum_{x \in \mathcal X} \exp(\sum_i w_in_i(x)) $$

例子

如图，本例中，我们有 4 条推理规则，每条推理规则的权重如左表所示。我们记目标事件为 \(x\)。

如果在 \(x \to {\mathrm {rule}}_i\) 为重言式（i.e. 恒真），则 \(n_i = 1\)，反之为 0。

  • 也就是，如果在 \(x\) 的前提下，推理规则一定会满足，那么，说明 \(x\) 大概也是要发生的。

image-20240107181908261

因果推理

do 算子： $$ \begin{aligned} \Pr(Y=y|X=x) &= \sum_z \Pr(Y=y|X=x,Z=z)\Pr(Z=z | X=x) \ \ \Pr(Y=y|do(X=x)) &= \sum_z \Pr_m(Y=y|X=x,Z=z)\Pr_m(Z=z | X=x) \ &= \sum_z \Pr(Y=y|X=x,Z=z)\Pr(Z=z) \ \end{aligned} $$ 其中，\(\Pr_m\) 为 manipulated probability（操纵概率），直观地说，对于下图：

image-20240107185113352

我们把图中的 \(X\) 操纵了（强迫其为 \(0, 1\)），从而 \(X\) 与 \(Z\) 失去了联系：

image-20240107185241892

从而，对于如下的数据：

image-20240107185438414

有： $$ \begin{aligned} &{ P ( Y = 1 | d o ( X = 1 ) ) } \=& P ( Y = 1 | X = 1 , Z = 1 ) P ( Z = 1 ) + P ( Y = 1 | X = 1 , Z = 0 ) P ( Z = 0 ) \ =& 0.93 \times \frac { ( 87 + 270 ) } { ( 350 + 350 ) } + 0.73 \times \frac { ( 263 + 80 ) } { ( 350 + 350 ) } = 0.832 \ &{ P ( Y = 1 | d o ( X = 0 ) ) } \=& P ( Y = 1 | X = 0 , Z = 1 ) P ( Z = 1 ) + P ( Y = 1 | X = 0 , Z = 0 ) P ( Z = 0 ) \ =& 0.87 \times \frac { ( 87 + 270 ) } { ( 350 + 350 ) } + 0.69 \times \frac { ( 263 + 80 ) } { ( 350 + 350 ) } = 0.7818 \ \ \ &{ P ( Y = 1 | X = 1 ) } \=& P ( Y = 1 | X = 1 , Z = 1 ) P ( Z = 1 | X = 1) + P ( Y = 1 | X = 1 , Z = 0 ) P ( Z = 0 | X = 1) \ =& 0.93 \times \frac { 87 } { 350 } + 0.73 \times \frac { 263 } { 350 } = 0.78 \ &{ P ( Y = 1 | X = 0 ) } \=& P ( Y = 1 | X = 0 , Z = 1 ) P ( Z = 1 | X = 0) + P ( Y = 1 | X = 0 , Z = 0 ) P ( Z = 0 | X = 0 ) \ =& 0.78 \times \frac { 270 } { 350 } + 0.69 \times \frac { 80 } { 350 } = 0.83 \end{aligned} $$ 在 \(do\) 算子的作用下，可以发现用药相比不用药，有一定的提升；而在没有 \(do\) 算子的情况下，则有显著的下降。

因此，通过干预手段，我们“强制”所有样本均用药/不用药，避免了男性用药少、女性用药多而造成的“辛普森悖论”情况。

决策树模型

我们希望通过树状模型进行决策，从而获得更好的可解释性。如何选择每一个节点呢？

我们可以通过“最小熵”原则来选择：

  • 如果对于决策树的某片树叶，其对应的划分集合仍然不纯（i.e. 没有完全将正反样本分开）
  • 则我们尝试继续添加决策条件
  • 对于每个候选决策条件，我们计算其每一个划分中的熵，并将其所有划分的熵加权平均，当作它的不纯度
  • 我们选择最纯的决策条件（i.e. 不纯度最低的决策条件）

比如：

原始情况下，一共 14 个样本，9 正 5 负。

现在，我有一个决策条件，为将年龄划分为 <20, 20~30 和 >30。

<20 20~30 >30
2+, 3- 4+, 0- 3+, 2-

则： $$ \begin{aligned} \mathrm{impurity} &= w_1 * \mathrm{impurity}_1 + w_2 * \mathrm{impurity}_2 + w_3 * \mathrm{impurity}_3 \ &= -\Biggl[(\frac 5 {14} (\frac 2 5\log \frac 2 5 + \frac 3 5\log \frac 3 5) + \frac 4 {14} (\frac 4 4\log \frac 4 4 + \frac 0 4\log \frac 0 4) + \frac 5 {14} (\frac 3 5\log \frac 3 5 + \frac 2 5\log \frac 2 5)\Biggr] \ &\approx 0.694 \end{aligned} $$ 我们可以（从待选划分方法中）选择不纯度最低的划分方法。本例中，第一次划分的最纯的决策条件就是“年龄”。

计算机逻辑设计

输入成本

  1. Literal Cost: 就是一个逻辑式里，有多少个变量
  2. Gate Input Cost: 就是一个逻辑式里，所有用到的逻辑门的 fan-in 的总和。分 \(G\)（不考虑非门）和 \(GN\)（考虑非门）。

标准型、POS、SOP

  1. 标准型就是 Maxterm, Minterm。因此，标准型下的和/积，就是 Sum of Minterm/Product of Maxterm。
  2. 可以在规定了 term 之间的顺序（如：alphabetical order）之后，使用简单的表示法
  3. e.g. \(ABC + \bar ABC + A\bar BC+\bar AB\bar C = \sum_m(2,3,5,7) = \overline{\overline{\sum_m(2,3,5,7)}} = \overline{\sum_m(0,1,4,6)} = \prod_M(0,1,4,6)\)
  4. POS 和 SOP 是标准型的积/和经过卡诺图的方式化简之后得到的最简结果

传播延迟

img

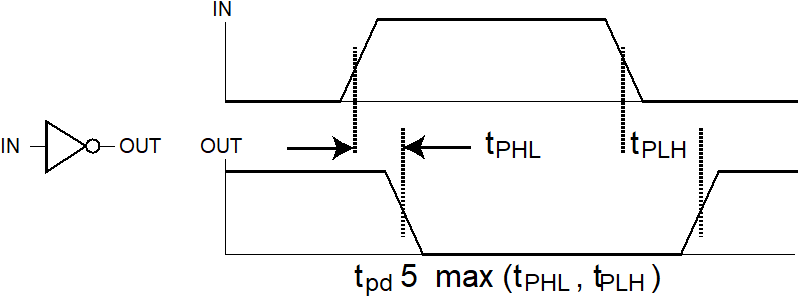
Delay Mode

  • Transport delay - a change in the output in response to a change on the inputs occurs after a fixed specified delay 输出整体往后移
  • Inertial delay - similar to transport delay, except that if the input changes such that the output is to change twice in a time interval less than the rejection time, the output changes do not occur. Models typical electronic circuit behavior, namely, rejects narrow “pulses” on the outputs 除了输出往后移，在惯性延迟下，很窄的脉冲（小于 rejection time）会被消除掉。

Circuit Delay

Example

img

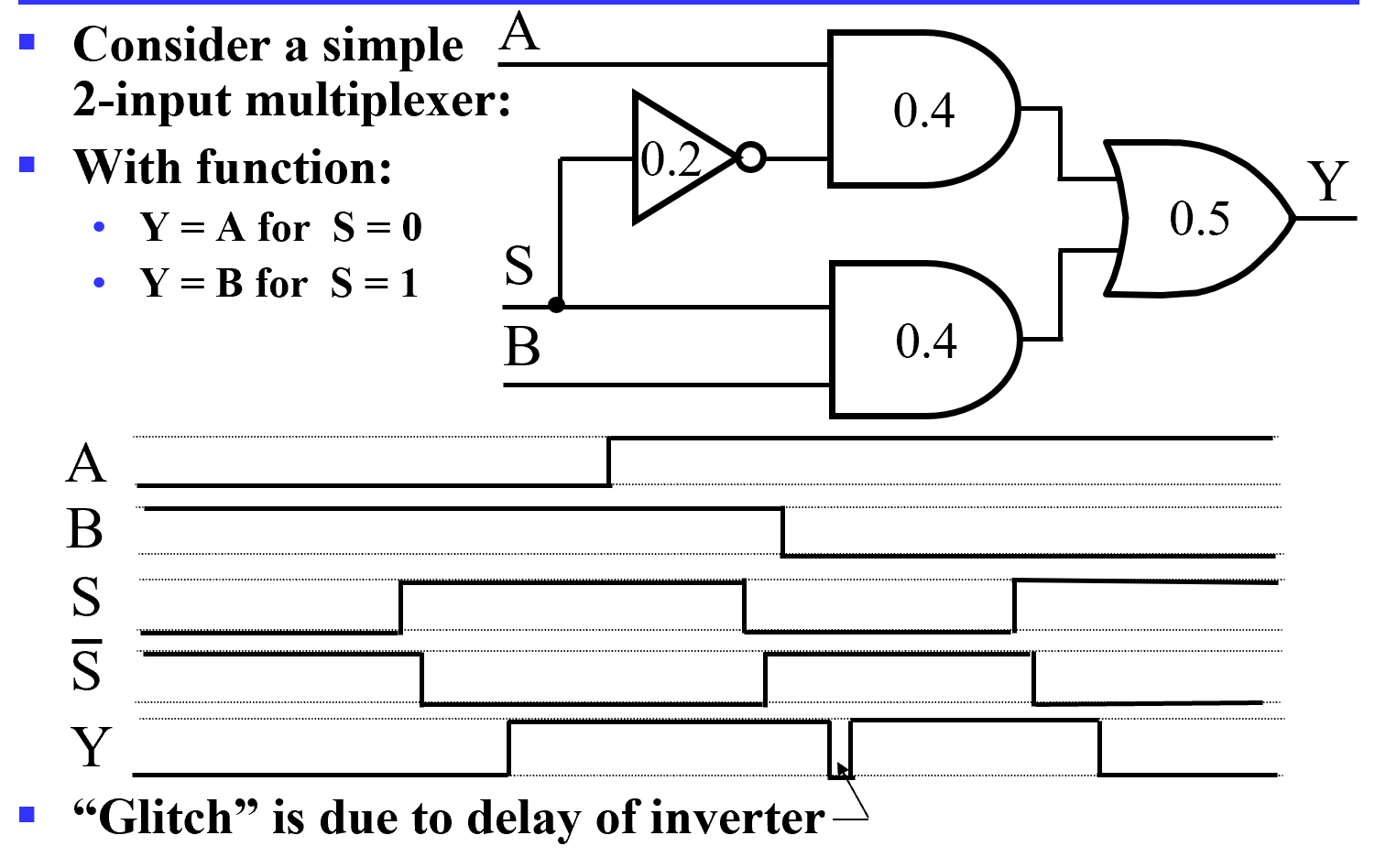
  • 最开始 S 由 0->1 后 0.9s Y 从 0->1
  • S 从 1->0 后下方的与门 0.4s 后会从 1->0, 但上方的与门 0.6s 后才会从 0->1. 但 0.9s 后 Y 才会 1->0, 此后再过 0.2s(共 1.1s) 后 Y 从 0-> 1. 这里 Y 出现了一个小尖峰，我们称之为电路产生的冒险。 S 的两条路径我们发现延迟不同，这种我们称之为电路中的竞争。

组合逻辑设计

Decoder

将 \(n\) 位编码“翻译”成 \(m\) 位独热编码（\(n \leq m \leq 2^n\)）。

朴素的 \(n\)-to-\(m\) 编码器的门输入成本为 \(nm\)（i.e. 每一个独热编码，都有一个等价于 \(n\)-input AND gate）

优化方法

如果采用行列译码，然后每一个独热编码用一个 2-input AND gate 并起来，则成本为 \(\frac n 2 \sqrt m + \frac n 2 \sqrt m + 2 * m\) 这一数量级，相比 \(nm\) 大大降低。只不过延迟增加一个门。

超前进位加法器

全加器的计算瓶颈就在进位处。

我们对全加器的每个 cell 的电路组成进行抽象： $$ \begin{align*} &P_i =A_i\oplus B_i, G_i = A_iB_i\

&\begin{aligned}
S_i=P_i\oplus C_i,\ C_i &= A_iB_i{C_{i-1}} + A_iB_i\overline{C_{i-1}} + A_i\overline{B_i}{C_{i-1}} + \overline{A_i}B_i{C_{i-1}} \\
&= A_iB_i(C_{i-1} + \overline{C_{i-1}}) + (A_i\overline{B_i} + \overline{A_i}B_i){C_{i-1}} \\
&= G_i + P_i C_{i-1}
\end{aligned}

\end{align*} $$ 因此： $$ C_k = G_{k} + P_k C_{k-1} = G_{k} + P_k (G_{k-1} + P_{k-1} C_{k-2}) = \cdots $$ 对于一个 4 位全加器：

img

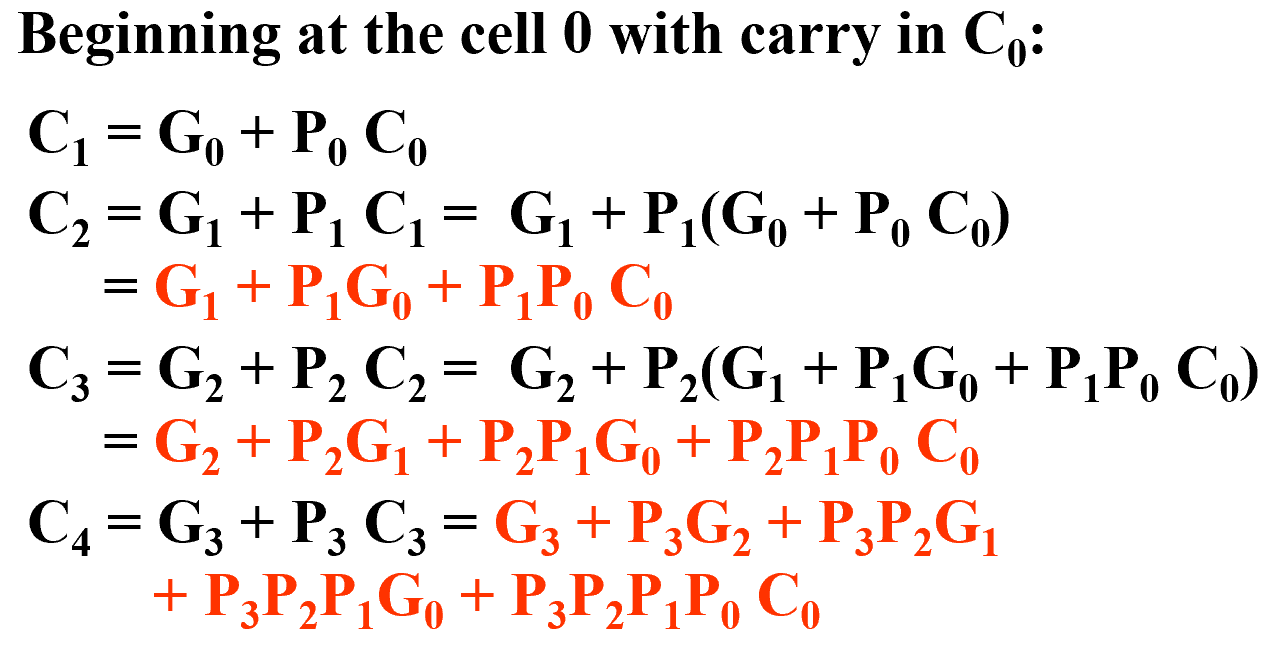
电路实现：

img

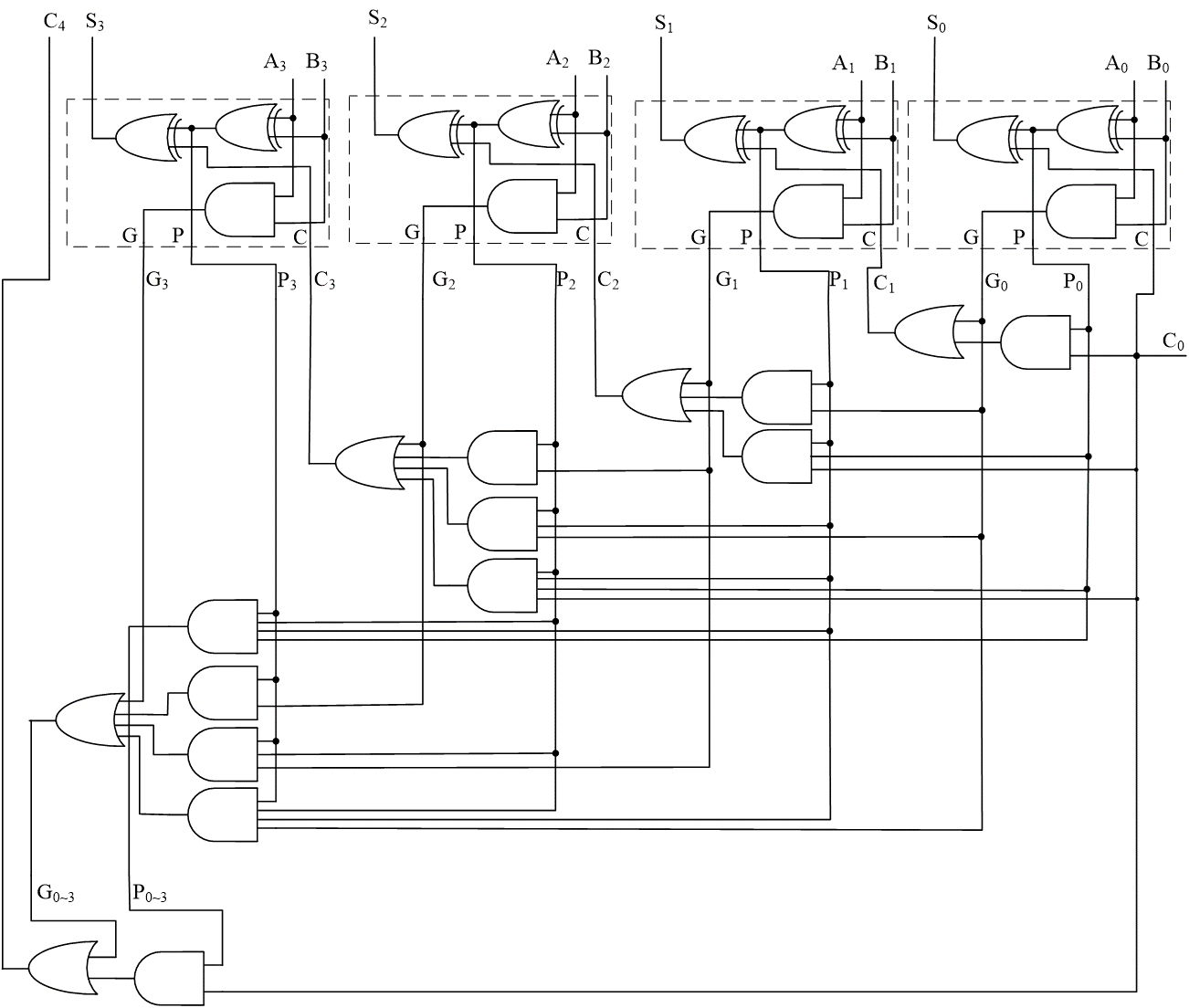
由于实际电路中，fan-in/fan-out 并不能任意大，因此，我们往往采用分级的方式：

img

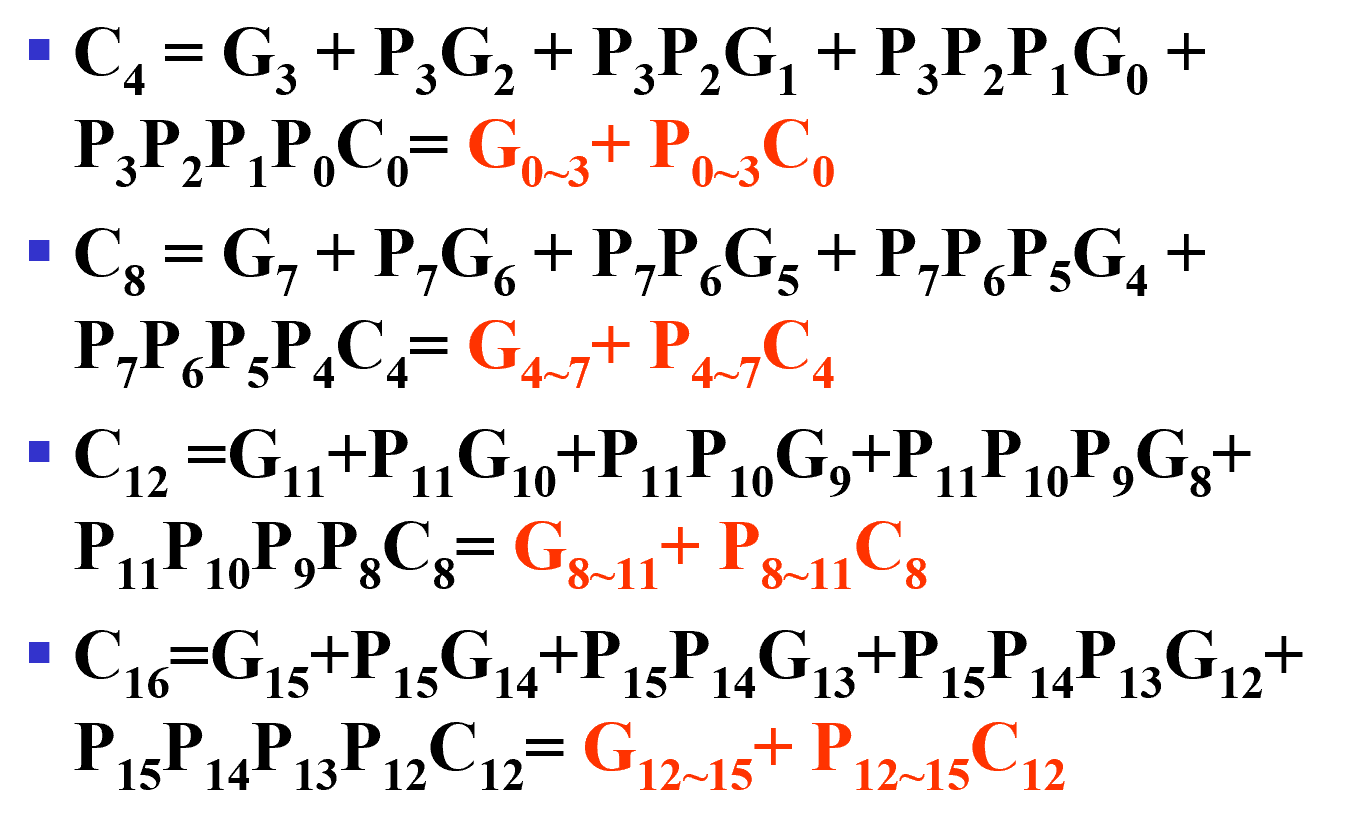
如图，该 16 位加法器中，最大的 fan-in 限制在了 5。