Skip to content

记录以下期末考试之前的复习内容。

人工智能基础

"In the field of artificial intelligence, while mathematics plays a significant role, it is not necessarily the most crucial aspect. Instead, the underlying philosophy and methodology behind mathematics holds greater importance." - M.T.Dickens (2024)

强化学习

Markov Decision Process

定义：马尔可夫决策过程 \(MDP = (S,A,P,R,\gamma)\)

其中

  • \(S\) 是状态集合
  • \(A\) 是动作集合。
  • \(P(S_{t+1}| S_t, A_t)\) 是状态转移概率。也就是在 \(S_t\) 状态下，做 \(A_t\) 动作后，状态转移到 \(S_{t+1}\) 的概率
  • \(R(S_t, A_t, A_{t+1})\) 是奖励函数。也就是在 \(S_t\) 状态下，做 \(A_t\) 动作后，状态转移到 \(S_{t+1}\) 时的奖励
  • \(\gamma\) 是折扣因子

例子

image-20240108155404195

交互过程

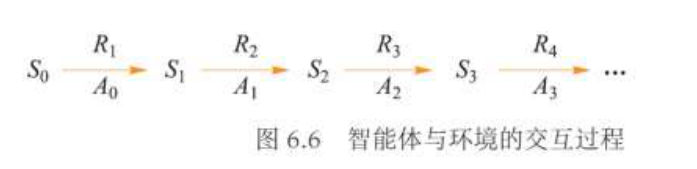
image-20240108155621048

如图，智能体从 \(S_0\) 开始，执行动作 \(A_0\)，得到奖励 \(R_1\)，状态转移到 \(S_1\)，再执行 \(A_1\)，得到奖励 \(R_2\)，状态转移到 \(S_2\)，……如此以往，测到一个状态序列 \((S_0, S_1, \cdots)\)。该序列称为轨迹（trajectory）。

轨迹可以是无线的，也可以有终止状态 \(S_T\)。 状态序列中包含终止状态的问题叫分段（episodic）问题，不包含终止状态的问题叫持续（continuing）问题。 在分段问题中，一个从初始状态到终止状态的完整轨迹称为一个片段（episode）。

强化学习定义

  • 策略函数 \(\pi: S \times A \to [0,1]\)，也就是智能体在状态 \(S\) 下采取行动 \(A\) 的概率。
  • 如果 \(\image\pi = \{0,1\}\)，那么该策略函数就是确定的。反之，就是概率性的。
  • 一个好的 \(\pi\)，应该能够最大化每一时刻的回报值：\(G_t = \sum_{i = 0}^{\infty} \gamma^i R_{t+1+i}\)
  • 价值函数 \(V: S \to \mathbb R\)。其中，\(V_\pi(s) = \mathbb E_\pi[G_t | S_t = s]\)

  • 也就是，在该状态下，采用策略 \(\pi\) 获得的期望值

  • 动作-价值函数 \(q: S \times A \to \mathbb R\)。其中，\(q_\pi(s,a) = \mathbb E_\pi[G_t | S_t = s, A_t = a]\)

  • 也就是，在该状态下，采用

Bellman 方程

\[ \begin{aligned} V_\pi(s) &= \mathbb E_\pi[G_t | S_t = s] \\ &= \mathbb E_\pi[G_t | S_t = s] \\ &= \sum_{a \in \mathcal A} \mathbb E_\pi[G_t | S_t = s, A_t = a] \pi(s,a) \\ &= \sum_{a \in \mathcal A} q_\pi(s,a) \pi(s,a) \\ \\ q_\pi(s,a) &= \mathbb E_\pi[G_t | S_t = s, A_t = a] \\ &= \sum_{s' \in \mathcal S} (R(s, a, s') + \gamma E_\pi[G_t | S_t = s']) P(s'|s,a) \\ &= \sum_{s' \in \mathcal S} (R(s, a, s') + \gamma V_\pi(s')) P(s'|s,a) \end{aligned} \]

因此，如果你预先知道了所有的 \(P\) 和 \(R\)，那么，任意策略 \(\pi\) 都可以解出来对应的 \(V_\pi(s)\) 和 \(q_\pi(s,a)\)。

各种算法

各种算法，我就不介绍了。我也不怎么喜欢这些算法。现在看来，幸亏当时没选人工智能专业。我现在对人工智能可以说是厌恶。看到人工智能（尤其是机器学习，不管是统计学习、在线学习还是强化学习）的东西就厌恶至极。

也许我应该及时止损，不能再跟着丁老师混了，也许图形学可以？也许编程理论？但一定不是跟人工智能相关的东西。同时，我并不知道未来的方向应该在何方……

普通物理学

电磁学

Gauss's Law for electric field (in vacuum): \(\oiint \vec E \cdot \mathrm dA = \frac q {\epsilon_0} \iff \nabla \cdot \vec E = \frac \rho {\epsilon_0}\)

Gauss's Law for magnetic field (in vacuum): \(\nabla \cdot \vec B = 0\)

Faraday's Law: \(\mathcal E = -\frac {\mathrm d \Phi_B} {\mathrm dt} \iff \nabla \times \vec E = - \frac {\partial \vec B} {\partial t}\)

Ampère's law with Maxwell's addition: \(\oint \vec B \cdot \mathrm d\vec s = \mu_0 I + \mu_0 \epsilon_0 \oint \frac {\partial \vec E} {\partial t} \cdot \mathrm d\vec A \iff \nabla \times \vec B = \mu_0 \vec J + \mu_0 \epsilon_o \frac {\partial \vec E} {\partial t}\)

  • Why need this addition? Think of the capacitor. When it's charge changes: $$ E = \frac U d = \frac Q {Cd}, I = -\frac {\partial Q} {\partial t}, C = \frac {\epsilon_0 S} d $$ Thus, calculate on the wire: \(\oint \vec B \cdot \mathrm ds = \mu_0 I\) To calculate on the plates: $ \oint \vec B \cdot \mathrm ds = \mu_0 \epsilon_0 \oint \frac {\partial \vec E} {\partial t} \cdot \mathrm d\vec A = \mu_0 \epsilon_0 \oint -\frac I {Cd} \cdot \mathrm d\vec A = -(-\mu_0 \epsilon_0 \frac {IS} {Cd}) = \mu_0 I$ So, the addition is necessary.

波动光学

\[ \begin{aligned} \widetilde E(\theta, t) = \int_{-\infty}^{\infty} \rho(x) e^{2\pi i\nu t} e^{2\pi i \frac {r(x,\theta)} \lambda} \mathrm dx \end{aligned} \]

根据 Fraunhofer 近似：\(r(x,\theta) \approx r(0,\theta) + x\sin\theta := r_0(\theta) + x\sin\theta\)，可得： $$ \begin{aligned} \widetilde E(\theta, t) &= \int_{-\infty}^{\infty} \rho(x) e^{2\pi i\nu t} e^{2\pi i \frac {r_0(\theta) + x \sin \theta} \lambda} \mathrm dx \ &= e^{2\pi i(\nu t + \frac {r_0(\theta)} \lambda )}\int_{-\infty}^{\infty} \rho(x) e^{2\pi i \frac {x\sin \theta} \lambda} \mathrm dx \end{aligned} $$ 从而： $$ I(\theta) = \left| \widetilde E(\theta, t) \right|^2 = \widetilde E(\theta, t) \overline{\widetilde E(\theta, t)} = e^0 \left|\int_{-\infty}^{\infty} \rho(x) e^{2\pi i \frac {x\sin \theta} \lambda} \mathrm dx \right|^2 = \left| (\mathscr F \rho) (\frac {\sin \theta} \lambda)\right|^2 $$ 令 \(p := \frac {\sin \theta} \lambda\)，则：\(I'(\rho) = I(\theta) = \left| (\mathscr F \rho) (\frac {\sin \theta} \lambda) \right|^2 \implies I' = \left| (\mathscr F \rho) \right|^2\)

衍射

\[ I(\theta) = \left| \int_{-a/2}^{a/2} e^{2\pi i p x} \mathrm dx \right|^2 = \left| \frac {1} {2 \pi i p} 2 \sin(\pi p a) \right|^2 \propto \frac {\sin^2(\pi p a)} {(\pi p a)^2} = \operatorname{sinc}^2(\pi p a) \]

因此，\(I(\theta) = I_0 \operatorname{sinc}^2 (\alpha),\ s.t.\ \alpha = \pi p a = \frac {a \pi \sin \theta } {\lambda}\)

干涉

\[ I(\theta) = \left| \int_{-\infty}^{\infty} e^{2\pi i px} (\delta(x-\frac d 2) + \delta(x+\frac d 2)) \mathrm dx \right|^2 = \left| e^{\pi i p d} + e^{\pi i p (-d)} \right|^2 \propto \cos^2(\pi p d) \]

因此，\(I(\theta) = I_0 \cos^2(\beta),\ s.t.\ \beta = \pi p d = \frac {d \pi \sin \theta } {\lambda}\)

光栅

\[ I(\theta) = \left| \int_{-\infty}^{\infty} e^{2\pi i px} \sum_{k=1}^N \delta(x - kd) \mathrm dx \right|^2 = \left| \sum_{k=1}^N e^{2\pi i p kd} \right|^2\ \]

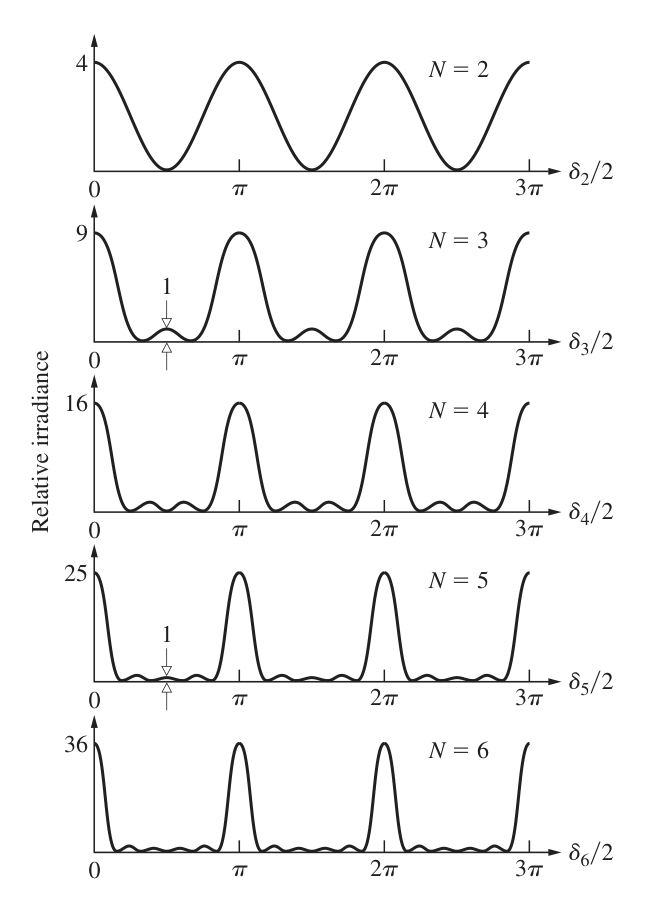
image-20240108180704165

注：\(\delta_N = \frac {2d \pi \sin \theta } {\lambda}\)。因此，对于不同波长的电磁波/光波而言，是不同的。

如图，当 \(N\) 较大时，光强分布就会更加“收束”。从而，可以达到分离不同波段光线的效果。

量子理论

Old Quantum Theory

爱因斯坦：光量子假说+光电效应

Einstein's Proton:

  • \(E = h\nu = h \frac \omega {2\pi} = \hbar \omega\)
  • \(p = \frac {h\nu} c = \frac h \lambda = \hbar k\)

从而，De Broglie 就进一步进行猜测：\(p = \frac h \lambda \iff \lambda = \frac h p\)

Bohr's hydrogen atom

Bohr 从巴尔末公式和量子化假设出发，对氢原子模型进行了推测。

Bohr 的氢原子模型有三个前提假设：

  1. 定态假设：原子系统只能处于一系列不连续的分立的能量状态 \(E_1, E_2, E_3, \dots\) 在这些状态下电子虽做加速运动，但不向外辐射能量。我们称这样的状态叫做定态。

  2. 频率条件：设两个定态 \(E_n\) 和 \(E_m\) ，并且 \(E_n>E_m\) 。

当从 \(E_n\) 跃迁到 \(E_m\) 的时，辐射电磁波。

当从 \(E_m\) 跃迁到 \(E_n\) 的时，吸收电磁波。

吸收和辐射点电磁波都符合关系： \(h\nu\) \(=E_n−E_m\)

其中 \(h\) 是普朗克常数。

  1. 角动量量子化：角动量应该有一个最小值。其余的角动量都是该最小值的整数倍。 我们根据巴尔末公式，可以推测出电子的角动量：\(L = m_ev_nr = n\hbar,\ s.t.\ n = 1,2,3,\cdots\) 因此最小值就是 \(\hbar\)。

因此，我们得到结论：

  1. 基态能量和轨道：\(E _ { R } = \frac { m e ^ { 4 } / ( 4 \pi \epsilon_0 ) ^ { 2 } } { 2 \hbar ^ { 2 } } = 13.6 e V, a_B = \frac {4\pi\epsilon_0\hbar^2} {me^2} = 0.529 \AA\)
  2. 能级能量：\(E_n = - \frac {E_R} {n^2}, r_n = n^2 a_B\)

尾注：Bohr 的猜测实际上是机缘巧合而已，也就是，氢原子的薛定谔方程解，恰好与 Bohr 的解一致。因此，

Modern Quantum Theory

Heisenburg's Uncertainty Principle

对于任意的粒子，先后测量时，都有： $$ \begin{align} &\Delta x \Delta p_x \geq \frac \hbar 2 \ &\Delta y \Delta p_y \geq \frac \hbar 2 \ &\Delta z \Delta p_z \geq \frac \hbar 2 \ \end{align} $$ 其中，\(\Delta\) 指的是测量时的标准差。

直观理解

任何粒子，在空间中，都是一个概率波。

如果概率波很集中（时域上），那么其傅里叶变换就很分散（频域上）；

如果概率波很分散，乃至成为空间中的一个正弦函数，那么其傅里叶变换就很集中，乃至成为一个单点 delta 函数。

imgimg

imgimg

imgimg

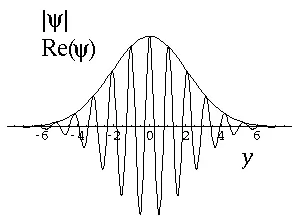
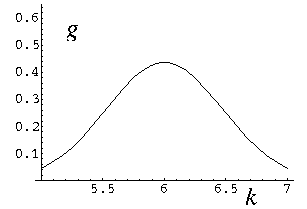
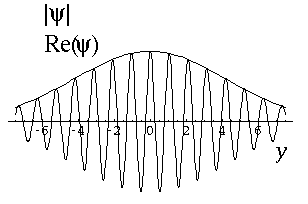
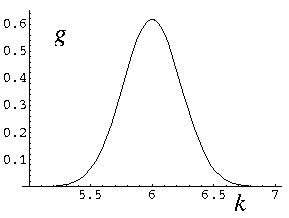
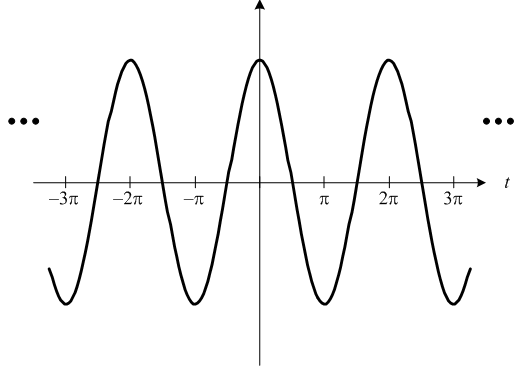
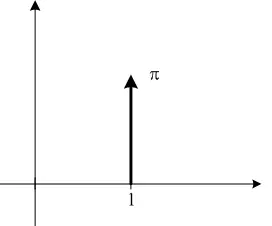
由于时域就是空间（坐标），频域就是频率，由 De Broglie's wave 可知和动量成正比，因此，就会有坐标和动量不可兼得。

（一维含时）薛定谔方程

Schrodinger 结合了旧量子理论的许多 ideas，提出了 Schrodinger's Equation。

1925年，薛定谔首先在德布罗意假说的基础上提出，用物质波的波函数来描述微观粒子运动状态，就像用电磁波描述光子运动一样（光子也有波粒二象性），即

  • 波函数 \(\Longrightarrow\) 微观粒子的运动状态
  • 薛定谔方程 \(\Longrightarrow\) 描述微观粒子运动基本方程

注意：薛定谔当时也不知道波函数的物理意义，他只是泛泛地把物质视为波，然后推导出了这一方程。最后，该方程地物理意义是由哥本哈根诠释所解释的——波的强度，就是测量是出现的概率。

所以，读者一开始也无需知道波具体为啥这样推得，只要跟着~我~薛定谔的 intuition 就好。

由 De Broglie 假设（注意，相比德布罗意波长，增加了一个普朗克-爱因斯坦关系式 \(\nu = \frac{E}{h}\)： $$ \begin{equation} \lambda=\frac{h}{p} \qquad \nu = \frac{E}{h} \end{equation} $$ 对于动量一定的粒子，其波就是单色平面波。

为了推导出具体的波函数，我们将粒子的波函数与单色平面机械波的波函数类比： $$ \begin{equation} y(x,t)=A\cos{2\pi (\nu t – \frac{x}{\lambda})}\end{equation} $$ 变成复数形式： $$ \begin{equation} \widetilde y(x,t)=Ae^{2\pi i(\nu t – \frac{x}{\lambda})}\end{equation} $$ 同时，波的强度正比于平方振幅 \(A^2\)：\(I \propto A^2 = \left|y\right|^2 = yy^*\)

对于粒子而言，我们记作： $$ \begin{equation} \Psi(x,t)=\Psi_0 e^{-2\pi i(\nu t – \frac{x}{\lambda})}\end{equation} $$ 其中，\(\Psi_0\) 就是振幅。

由 De Broglie 假设，我们进行简化： $$ \begin{equation} \Psi(x,t)=\Psi_0 e^{-2\pi \frac i h(E t – p x)} = \Psi_0 e^{- \frac i \hbar(E t – p x)}\end{equation} $$

下面，我们为了得到真正的波函数，因此进行推导：

\(\Psi\) 对 \(t\) 求偏导： $$ \begin{equation}    \frac{\partial{\Psi(x,t)}}{\partial t}=-\frac{iE}{\hbar}\Psi_0 e^{-\frac{i}{\hbar} (Et – px)}=-\frac{iE}{\hbar}\Psi(x,t) \end{equation} $$ 对 \(x\) 求二阶偏导： $$ \frac{\partial^2 \Psi(x,t)}{\partial x^2} = -\frac{p^2}{\hbar^2}\Psi(x,t) $$

对两式分别乘以一个系数， $$ \begin{align} i\hbar\frac{\partial{\Psi(x,t)}}{\partial t} &= E{\hbar}\Psi(x,t) \ -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi(x,t)}{\partial x^2} &= \frac{p^2}{2m}\Psi(x,t) \end{align} $$ 由于 \(v \ll c\)，因此不考虑相对论效应。经典动能-动量关系为： $$ E - E_p = E_k = \frac{1}{2} mv^2 = \frac {p^2} {2m} $$ 因此： $$ i\hbar\frac{\partial{\Psi(x,t)}}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi(x,t)}{\partial x^2} + E_p(x,t)\Psi(x,t) $$ 称为一维运动粒子含时薛定谔方程。

  • 如果 \(E_p \equiv 0\)，则 $$ i\hbar\frac{\partial{\Psi(x,t)}}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi(x,t)}{\partial x^2} $$ 称为：一维自由粒子含时薛定谔方程

一维不含时薛定谔方程

对于 \(E_p\) 只与 \(x\) 相关的情况，我们希望能够对 \(\Psi\) 分离变量，即：\(\Psi(x,t) = \psi(x)\varphi(t)\)

从而： $$ \begin{align} & i\hbar\frac{\partial{\psi(x)\varphi(t)}}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \psi(x)\varphi(t)}{\partial x^2} + E_p(x)\psi(x)\varphi(t) \ & i\hbar\frac{1}{\varphi(t)}\frac{\partial{\varphi(t)}}{\partial t} = \frac{1}{\psi(x)}\left(-\frac{\hbar^2}{2m}\frac{\partial^2 \psi(x)}{\partial x^2} + E_p(x)\psi(x)\right) \ \end{align} $$ 对于左右两侧，容易发现，如果只改变右边的 \(x\)，保持左侧的 \(t\) 不变，则左侧为常数，右侧在 \(x\) 改变的情况下仍然为常数，从而 RHS 为（关于 \(x\) 的）常函数；LHS 由对称性同理。

从而： $$ i\hbar\frac{1}{\varphi(t)}\frac{\partial{\varphi(t)}}{\partial t} = \frac{1}{\psi(x)}\left(-\frac{\hbar^2}{2m}\frac{\partial^2 \psi(x)}{\partial x^2} + E_p(x)\psi(x)\right) = E $$

  • 注意：这里的 \(E\) 就是能量，可以由上面的公式 \((12)\) 推得。如下： $$ \frac{\partial{\Psi(x,t)}}{\partial t}=-\frac{iE}{\hbar}\Psi(x,t) \iff \ i\hbar\frac{1}{\Psi(x,t)}\frac{\partial{\Psi(x,t)}}{\partial t}=E \iff \ i\hbar\frac{1}{\varphi(t)}\frac{\partial{\varphi(t)}}{\partial t}=E $$

我们先解 LHS： $$ \varphi(t) = \varphi_0 e^{-\frac{iEt}{\hbar}} $$ 也就是：随着时间，相位变化但是幅度不变（也就是对波的振幅没有任何影响）。符合直觉。

而 RHS，就是： $$ -\frac{\hbar^2}{2m}\frac{\partial^2 \psi(x)}{\partial x^2} + E_p(x)\psi(x) = E \psi(x) $$ 对于简单、经典的情况，一般解为： $$ \psi(x) = Ae^{ik(x)x} + Be^{-ik(x)x} s.t. k = \frac{\sqrt{2(E-E_p(x))m}}{\hbar} $$ 同时，\(\psi\) 可能还需要满足一些连续/可导的条件。

  • 注：习惯上，我们把 \(E_p(x)\) 称为 \(V(x)\)

高维含时薛定谔方程

对于高维的情况，我们只需要对方程稍加修改即可。具体地： $$ i\hbar\frac{\partial{\Psi(\mathbf x,t)}}{\partial t} = -\frac{\hbar^2}{2m} \nabla\cdot\nabla \Psi(\mathbf x,t) + E_p(\mathbf x,t)\Psi(\mathbf x,t) $$ 其中，\(\nabla \cdot \nabla\) 就是拉普拉斯算符，也就是 \(\sum_i \frac{\partial^2 \Psi}{\partial x_i^2}\)。

对于方程的变种，也类似地进行修改即可。

哥本哈根诠释

波函数幅值的模长平方就是粒子在 \(t\) 时刻出现在 \(x\) 处的概率密度。因此，除了要满足方程，还要满足概率的归一化条件： $$ &\int_{-\infty}^{+\infty} \left| \psi(x)\varphi(t) \right|^2 \mathrm dt = \int_{-\infty}^{+\infty} \left| \psi(x) \right|^2 \left| \phi(t) \right|^2 \mathrm dt = \int_{-\infty}^{+\infty} \left| \psi(x) \right|^2 \varphi_0^2 \mathrm d t = 1 \iff \ & \int_{-\infty}^{+\infty} \left| \psi(x) \right|^2 \mathrm dt = 1, s.t. \varphi_0 = 1 $$

（一维不含时）例子：无穷位势垒

假设一个粒子被困在一个无穷位势垒内部（即使不是无穷，如果很大，波函数也会指数级衰减，所以可以近似为无穷），则： $$ V(x) = \left{ \begin{array}{ll} 0 & \text{if } 0 \leq x \leq a, \ \infty & \text{otherwise}. \end{array} \right. $$ 从而，波函数在 \([0,a]\) 之外，显然为 \(0\)。

波函数在 \([0,a]\) 之内，由于要满足连续性，i.e. $$ \begin{aligned} \psi(0) &= 0 \ \psi(a) &= 0 \ \end{aligned} $$ 从而： $$ A + B = 0, Ae^{ika} + Be^{ika} = 0 \implies 2A\sin(ka) = 0 \implies k = \frac{\pi n}{a} \text{ (Since } A \neq 0) \implies E_k = E = \frac{n^2h^2}{8ma^2} $$ 可以看到，被允许的能量是分立的，且与动量成。因此能量呈现量子性。

不仅如此，由于 \(E_k = \frac {p^2} {2m}\)，故 \(p = \frac{nh}{2a}\)。我们从而求出了“单位动量”，所有动量都是 \(\frac{nh}{2a}\) 的整数倍。