计算机逻辑设计
时序逻辑电路
锁存器(Latch)和触发器(Flip-Flop)
特点
锁存器(Latch)无需接入 clk,是一个 asynchronized storage。
触发器(Flip-Flop)需要接入 clk,依靠 clk 来协调同步状态转移。
描述方式
- Used in analysis
已知触发器的输入和现态,预测触发器的输出和次态
- Characteristic table - defines the next state of the flip-flop in terms of flip-flop inputs and current state
-
Characteristic equation - defines the next state of the flip-flop as a Boolean function of the flip-flop inputs and the current state
-
Used in design
已知现态和次态,预测我们要提供怎样的输入
- Excitation table(激励表) - defines the flip-flop input variable values as function of the current state and next state
S-R 触发器
Characteristic Table
| S | R | \(Q(t+1)\) | Operation |
|---|---|---|---|
| 0 | 0 | \(Q(t)\) | Keep |
| 0 | 1 | 0 | Reset |
| 1 | 0 | 1 | Set |
| 1 | 1 | ? | Invalid Operation |
Characteristic Equation
\(Q(t+1)\) 的卡诺图
| SR\\(Q(t)\) | 0 | 1 |
|---|---|---|
| 00 | 0 | 1 |
| 01 | 0 | 0 |
| 11 | X | X |
| 10 | 1 | 1 |
化简之后,得到: $$ Q(t+1) = S + \overline RQ(t) $$ Excitation Table
| \(Q(t)\) | \(Q(t+1)\) | S | R | Operation |
|---|---|---|---|---|
| 0 | 0 | 0 | X | Keep / Reset |
| 0 | 1 | 1 | 0 | Set |
| 1 | 0 | 0 | 1 | Reset |
| 1 | 1 | X | 0 | Keep / Set |
D 触发器
D 触发器,本质上就是 S-R 触发器再外加一个 1-2 Decoder。
Characteristic Table
| D | \(Q(t+1)\) | Operation |
|---|---|---|
| 0 | 0 | Reset |
| 1 | 1 | Set |
Characteristic Equation $$ Q(t+1) = D + \overline {\overline D} Q(t) = D $$ Excitation Table
| \(Q(t)\) | \(Q(t+1)\) | S | R | Operation |
|---|---|---|---|---|
| 0 | 0 | 0 | X | Keep / Reset |
| 0 | 1 | 1 | 0 | Set |
| 1 | 0 | 0 | 1 | Reset |
| 1 | 1 | X | 0 | Keep / Set |
T 触发器
T 触发器,就是一个只能翻转和保持的触发器。
- 实际使用中,初值由电位噪声随机生成。
Characteristic Table
| T | \(Q(t+1)\) | Operation |
|---|---|---|
| 0 | \(Q(t)\) | Keep |
| 1 | \(\overline{Q(t)}\) | Complement |
Characteristic Equation $$ Q(t+1) = Q(t) \oplus T $$ Excitation Table
| \(Q(t)\) | \(Q(t+1)\) | T | Operation |
|---|---|---|---|
| 0 | 0 | 0 | Keep |
| 0 | 1 | 1 | Complement |
| 1 | 0 | 1 | Complement |
| 1 | 1 | 0 | Keep |
JK 触发器
JK 触发器,本质上就是 S-R 触发器外加一个 Complement 位(可以保证所有输入都是 valid)。可以说是集齐了上述所有触发器的功能。
Characteristic Table
| J | K | \(Q(t+1)\) | Operation |
|---|---|---|---|
| 0 | 0 | \(Q(t)\) | Keep |
| 0 | 1 | 0 | Reset |
| 1 | 0 | 1 | Set |
| 1 | 1 | \(\overline Q(t)\) | Complement |
Characteristic Equation
\(Q(t+1)\) 的卡诺图
| JK\\(Q(t)\) | 0 | 1 |
|---|---|---|
| 00 | 0 | 1 |
| 01 | 0 | 0 |
| 11 | 1 | 0 |
| 10 | 1 | 1 |
化简之后,得到: $$ Q(t+1) = J\overline {Q(t)} + \overline K Q(t) $$
Excitation Table
| Q(t) | Q(t+1) | J | K | Operation |
|---|---|---|---|---|
| 0 | 0 | 0 | X | Keep / Reset |
| 0 | 1 | 1 | X | Set / Complement |
| 1 | 0 | X | 1 | Reset / Complement |
| 1 | 1 | X | 0 | Keep / Set |
状态机
状态表
- Present State – the values of the state variables for each allowed state.
- Input – the input combinations allowed.
- Next-state – the value of the state at time \((t+1)\) based on the present state and the input.
- Output – the value of the output as a function of the present state and (sometimes) the input.
Example 1:
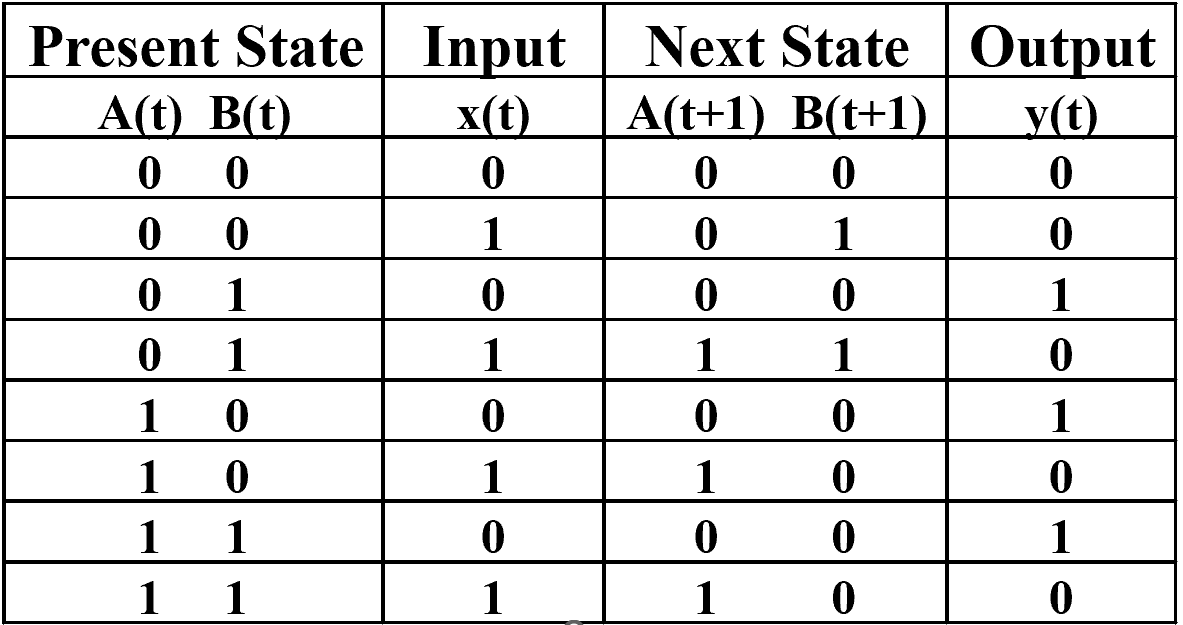
Example 2:
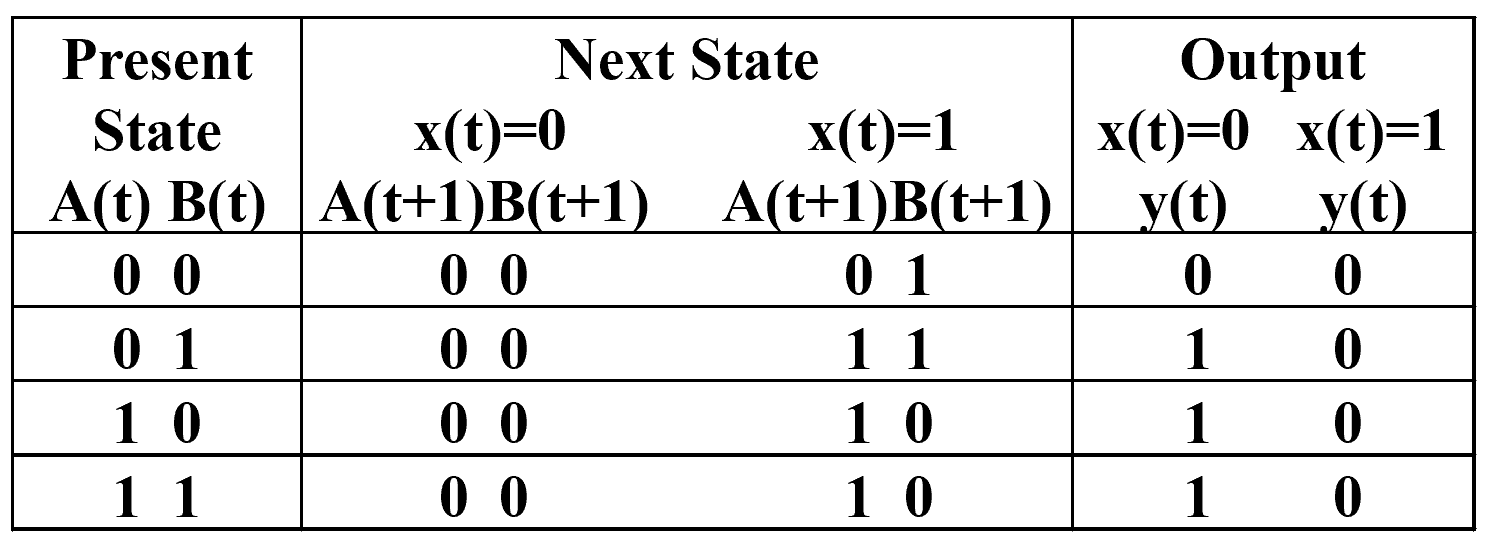
注意:即使某个状态理论上无法达到,也需要在表中写出。因为实际情况下,电路可能会因为一些 error 而达到那个状态。
状态图
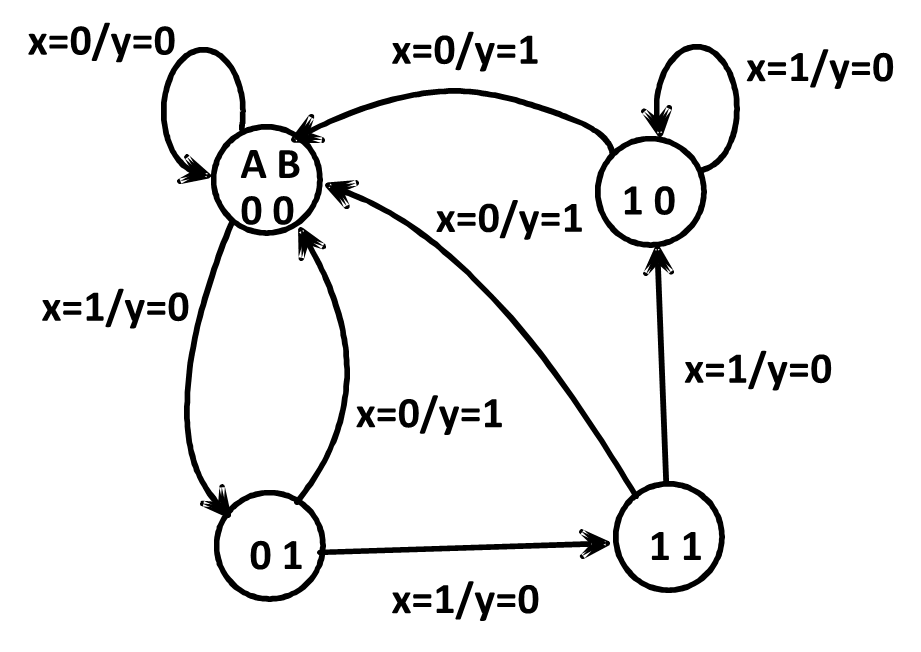
化简
状态等效的三种情况:
- 首先,输出相同
- 其次,次态相同、交错、循环
当然,更好的方式,就是用隐含表来化简
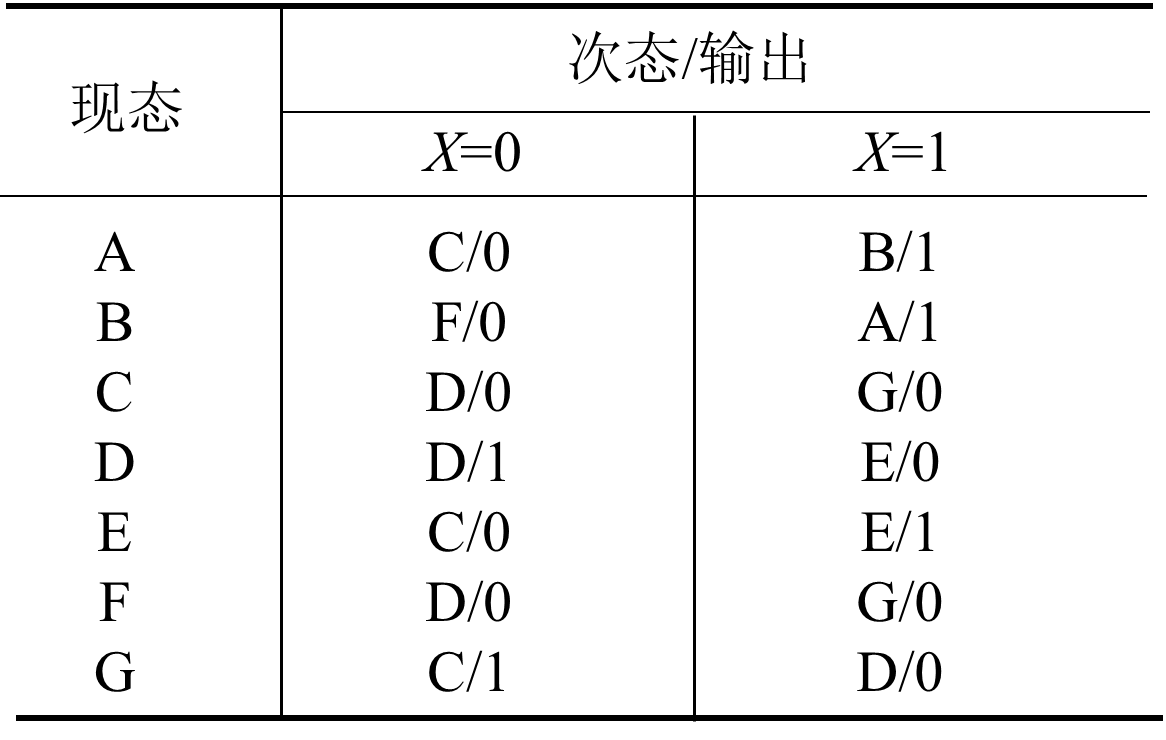
以上图为例,依照输出,我们对状态进行归类:
\(\left\{C, F\right\},\left\{A, B, E\right\},\left\{D, G\right\}\)
并且: $$ \begin{aligned} &C = F \ &A = B \iff C = F \land B = A \iff C = F \ &B = E \iff C = F \land A = E \ &D = G \iff C = D \land E = D \ \end{aligned} $$ 也就是:
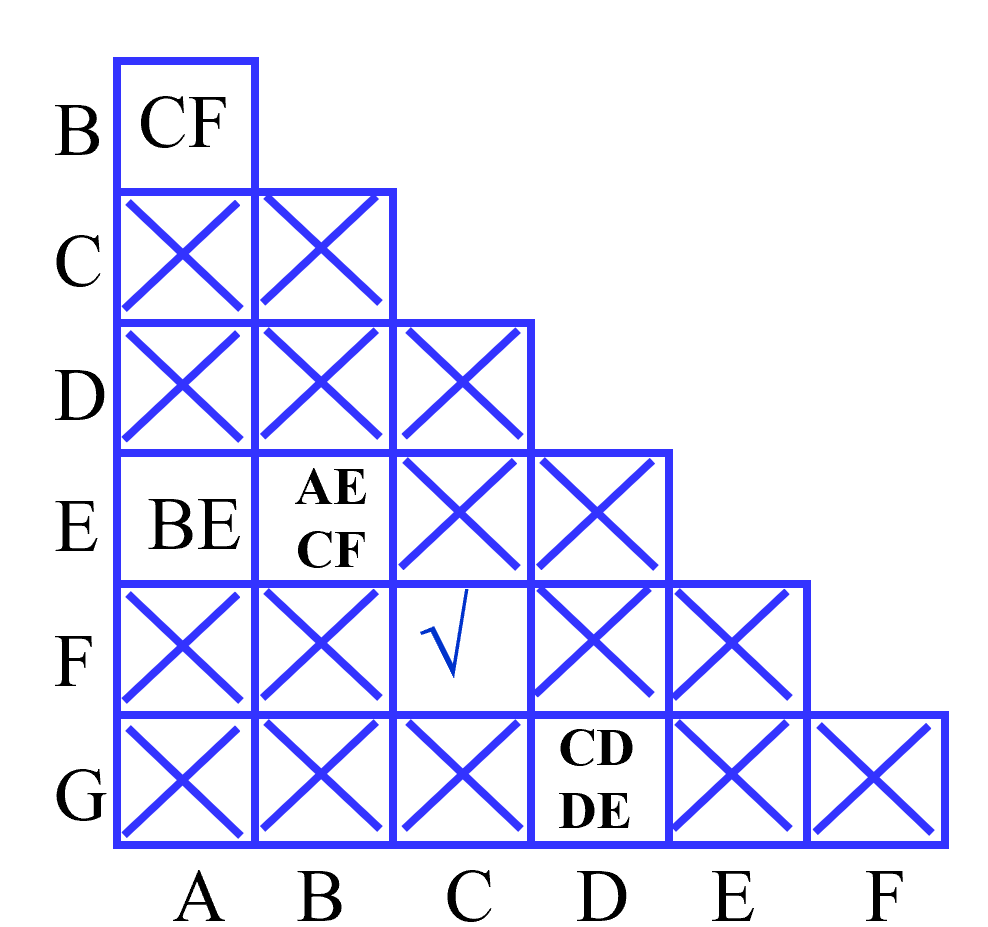
从而,不难推出: $$ C = F, A = B = E, D \neq G $$ 从而,最后可以化简到 4 个状态:
\(\left\{C, F\right\},\left\{A, B, E\right\},\left\{D\right\},\left\{G\right\}\)
可编程技术
采用对接触点的熔断,进行一次性编程。
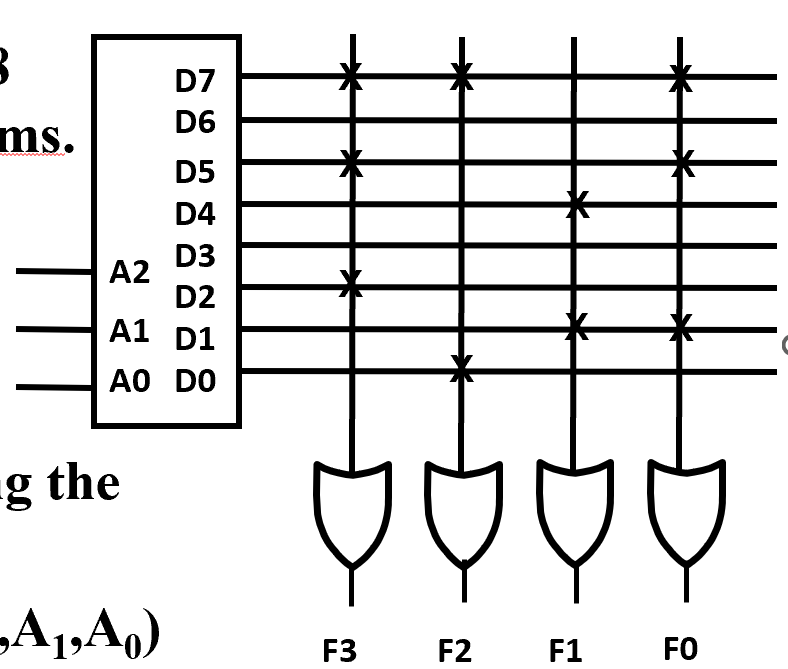
ROM
or 逻辑可编程。
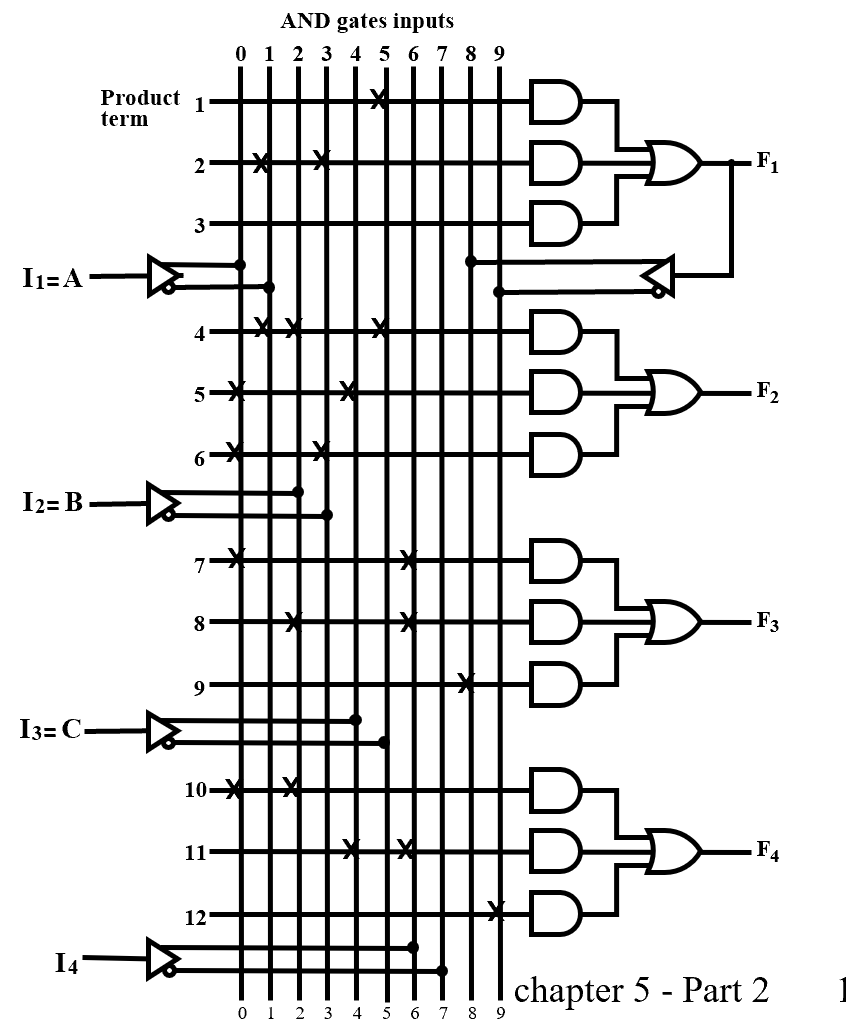
Programmable Array Logic (PAL)
and 逻辑可编程。
缺点:
- 某些函数可能使用一个 PAL 上的函数元件无法实现
- 此时可以采用多级电路
优势:
- 不难发现,对于 \(N\) 输入,我们若使用 ROM,则需要 \(2^N\) 条线。若使用 \(PAL\),则只需 \(N\) 条线。
- 如果有 \(M\) 个函数,则总共需要 \(kNM\) 个接触点,\(k\) 为每个函数最多可用的
and数。 - 相比 ROM 的 \(2^NM\) 是大大的提升
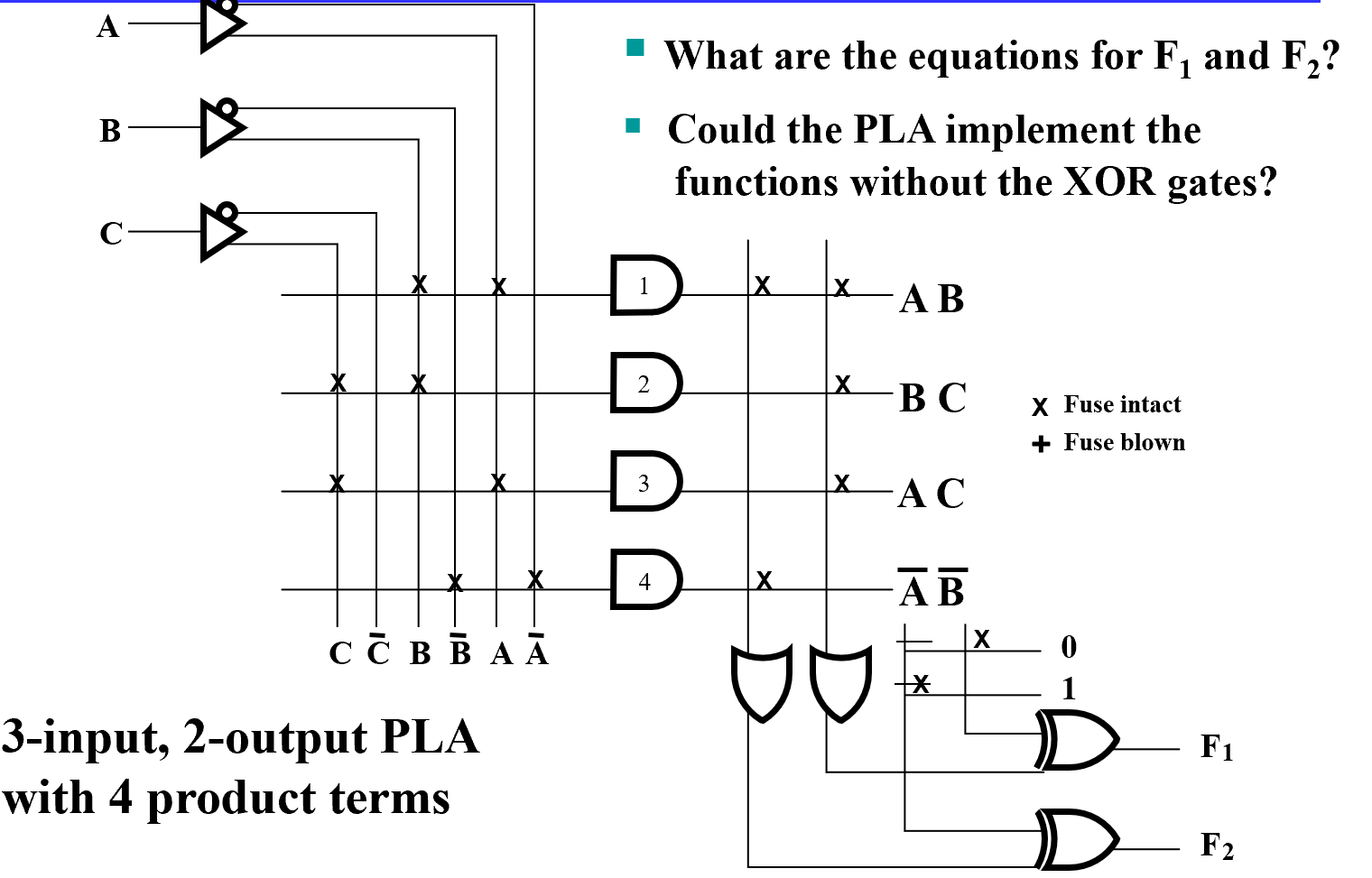
Programmable Logic Array (PLA)
本质上,就是一个 "Sum of \(k\) Products"(而非 ROM 的 "Sum of All Minimum Terms, i.e. \(2^N\) Products")。结构和 ROM 类似,但是比 ROM 小得多。
- 优点:
- PLA (可编程逻辑阵列) 可以具有大的 N 和 M,可以实现对于只有有限输入 N 的只读存储器 (ROM) 来说不实际的方程。
- PLA 的所有乘积项都可以连接到所有输出,克服了 PAL (可编程阵列逻辑) 的有限输入问题。
-
一些 PLA 的输出可以进行补码运算,添加了 POS (积和和积) 功能。
-
缺点:
- 通常情况下,乘积项的数量限制了 PLA 的应用。
- 需要进行两级多输出优化,以减少实现中乘积项的数量,从而使其适应 PLA。
- PAL 具有多级电路能力,而 PLA 中没有。PLA 需要外部连接来实现多级电路。
内存基础
Make RAM Larger
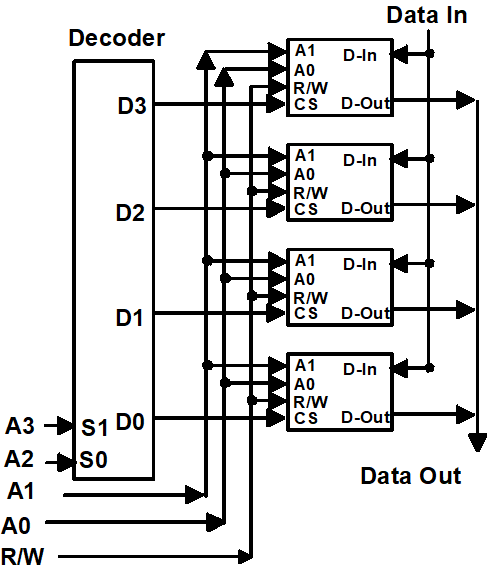
可以看到,上图中,我们增加了 A2, A3 两位,通过一个 2to4 decoder,负责选择激活哪一个
也就是:高位输入用来选择 RAM 芯片(输出是高阻态),低位输入用来选择对应芯片的 Cell.
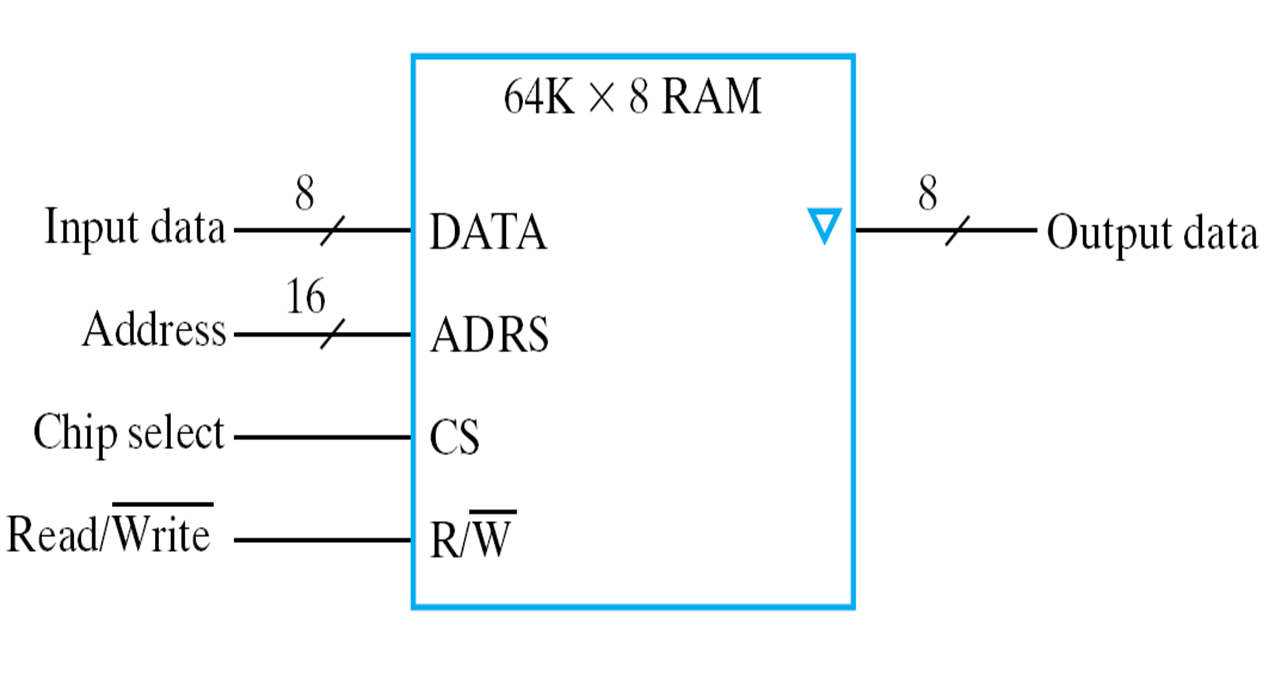
Make RAM Wider
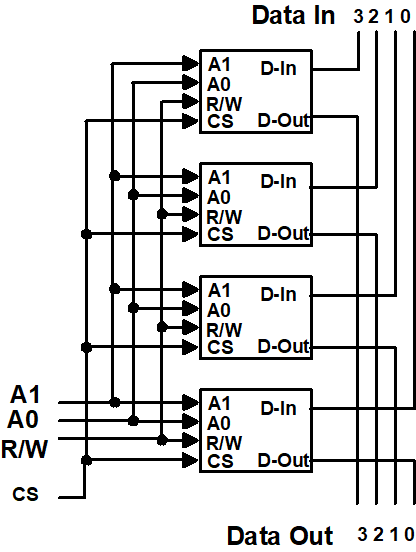
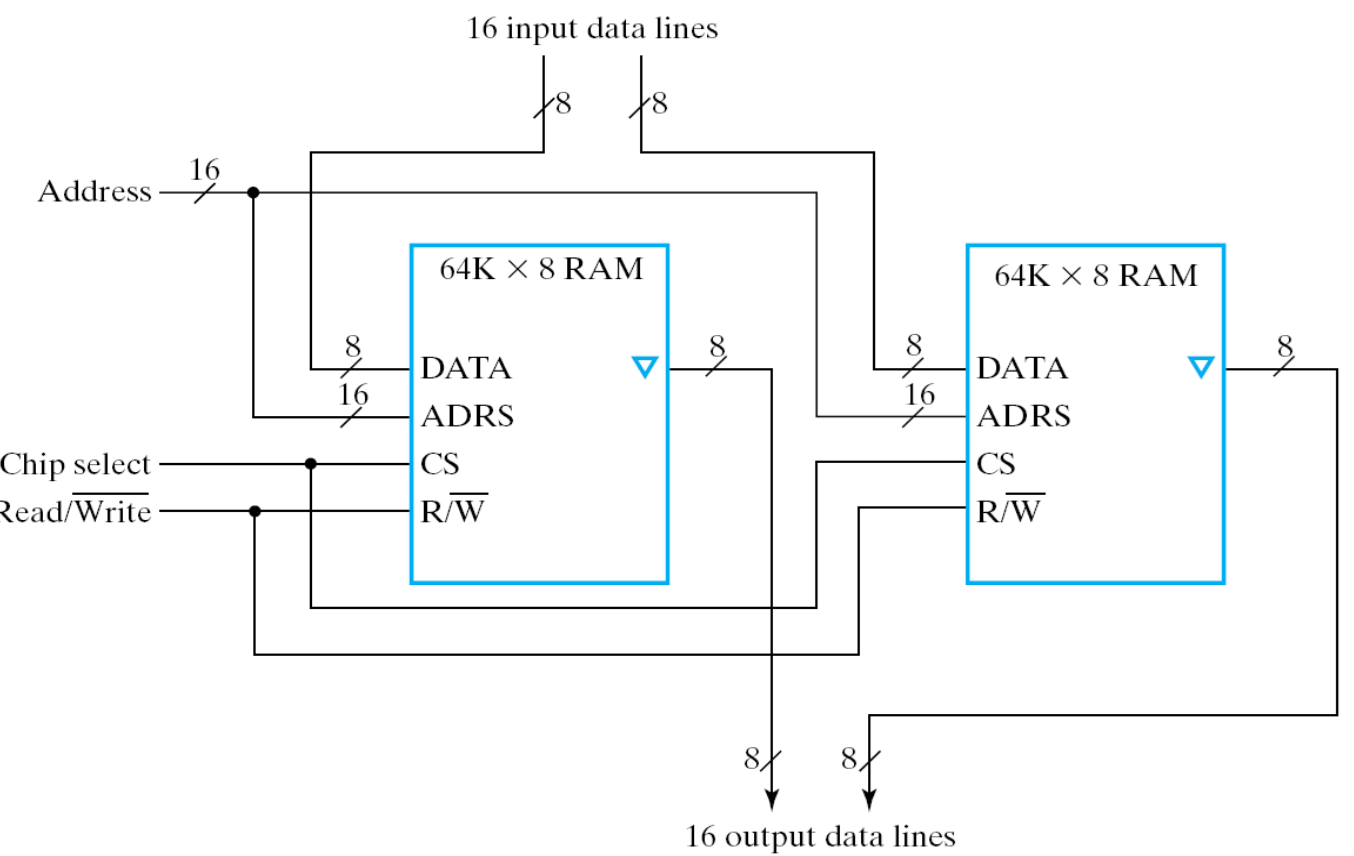
可以看到,左图中,Data In 和 Data Out 都被拓展到了 4-bit。
SRAM 和 DRAM 的读取
SRAM
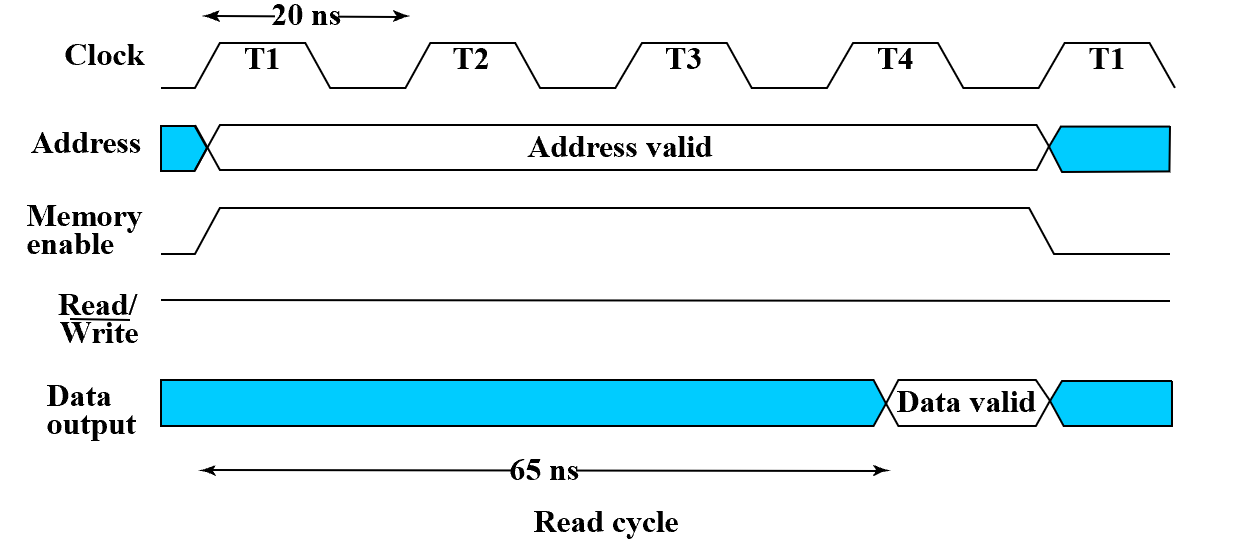
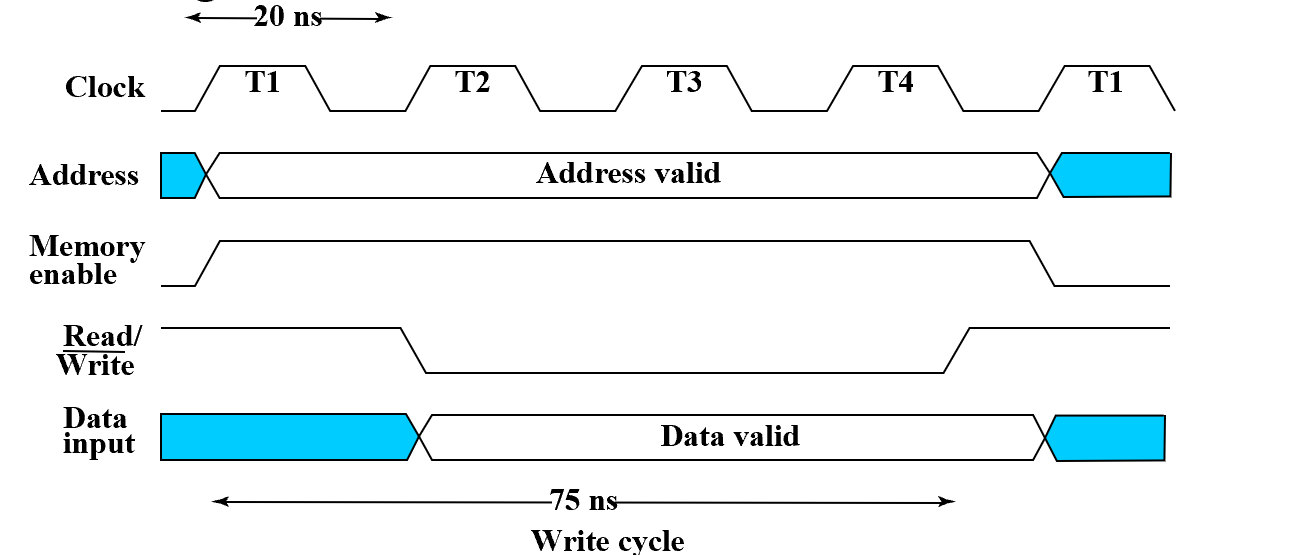
大多数 SRAM 操作是异步的。因为 SRAM 就是事件驱动的——数据给到了,我就改变。
- 当然,改变需要时间,但是与时钟周期无关。
DRAM
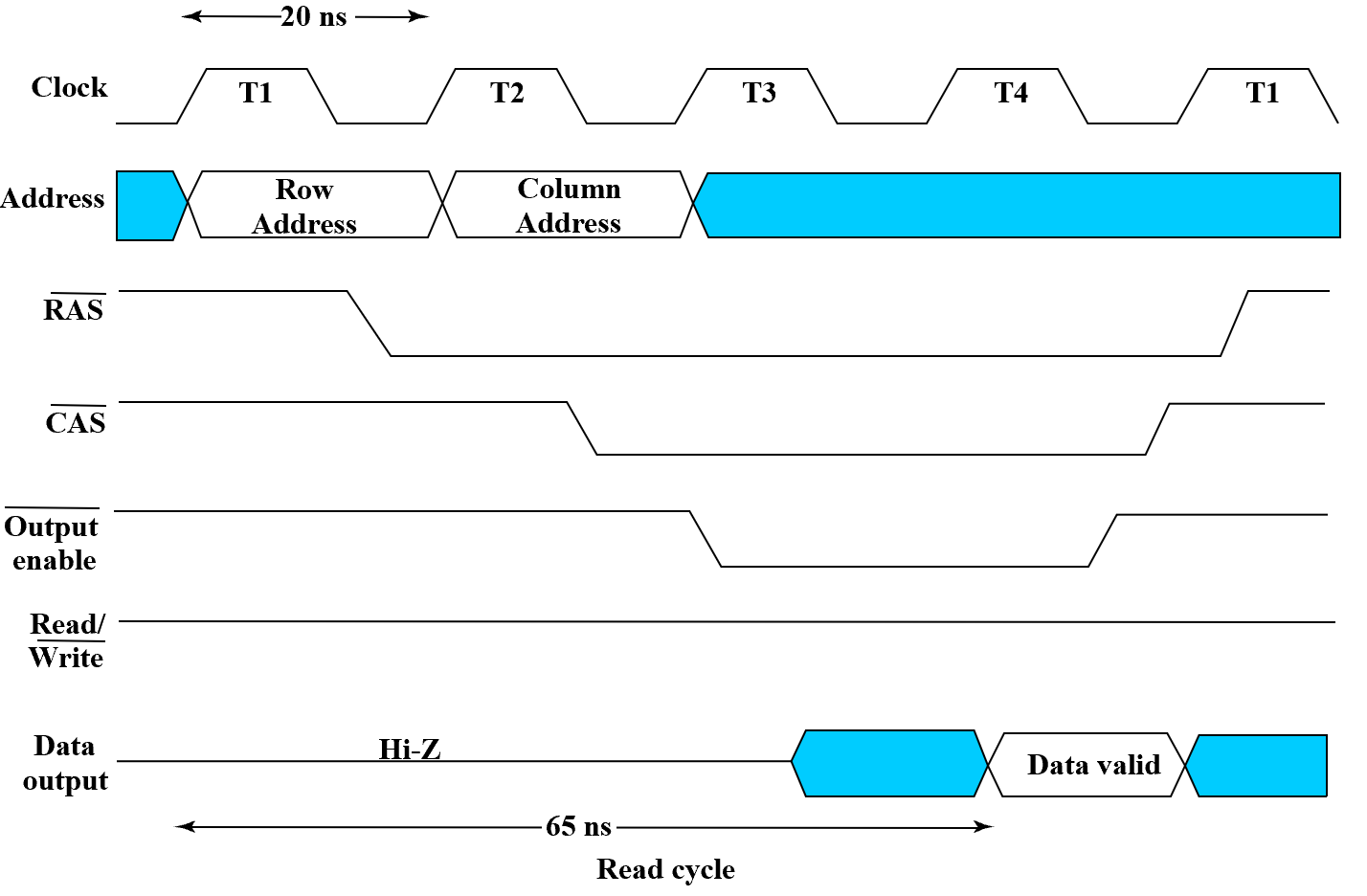
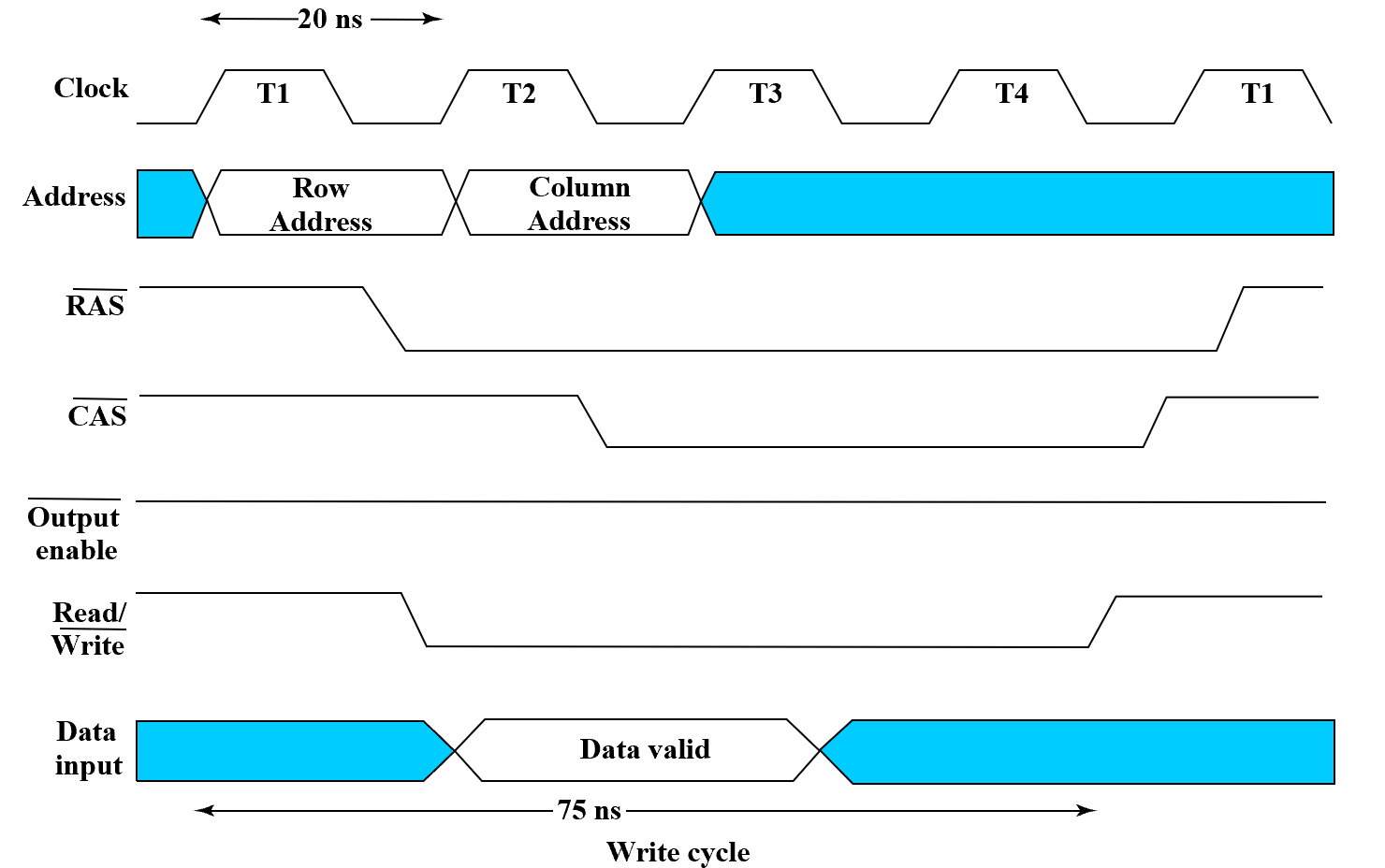
DRAM 操作是同步的。因为 DRAM 的电容需要隔几个时钟周期之后同步刷新,而且行列是分开送入的(怎样分开?靠时钟上升沿),因此需要同步刷新、送数据。
DRAM
- 读写时,会破坏数据。
- 将所有的 DRAM 输出接到 Sense Amplifier 上,可以让破坏性读入变为非破坏性读入。
- 需要做定时刷新(电容会自己放电)
- Refresh Controller and Refresh Counter
DRAM 结构
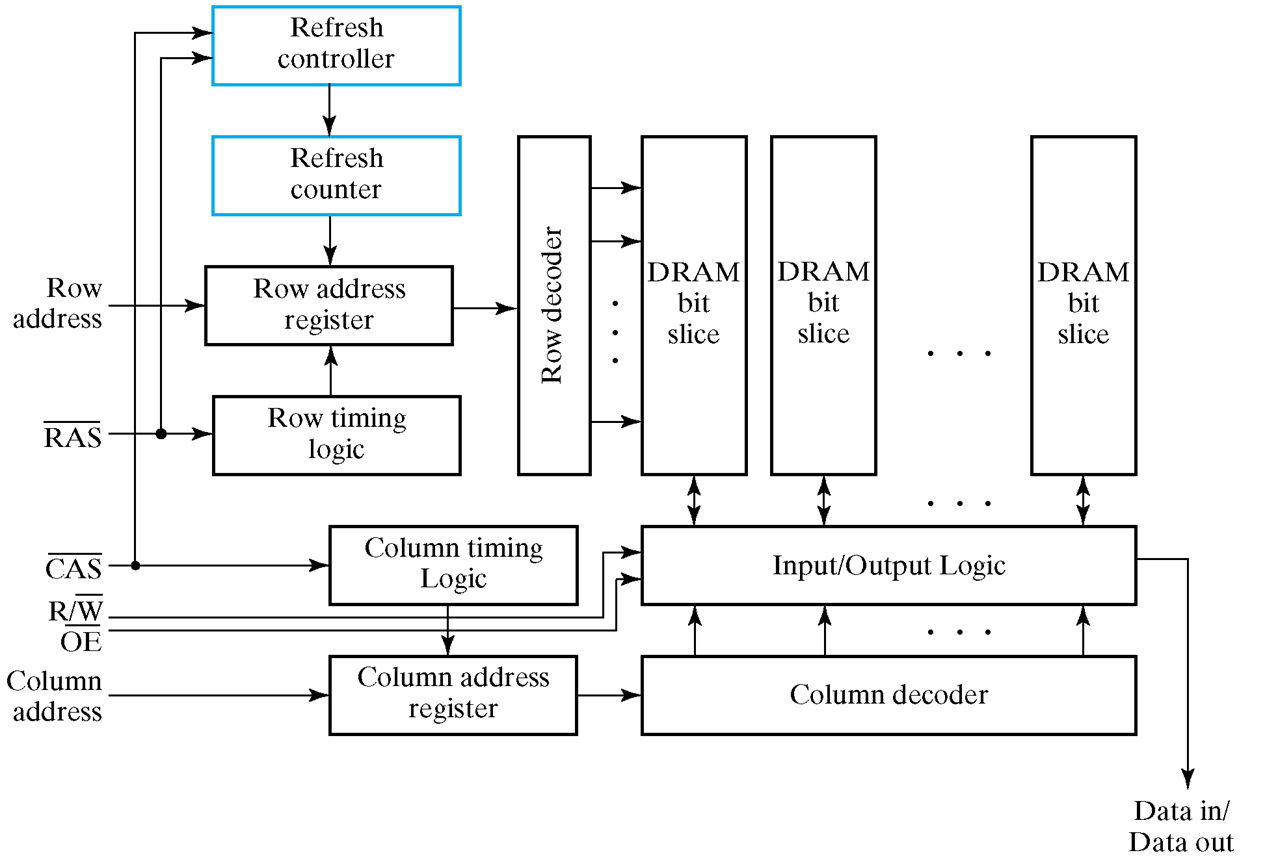
如图,DRAM 适用于大型的 RAM。由于 DRAM 可以紧密排布且价格便宜,因此被广泛应用于大型 RAM 之中。
为了进一步减小线路体积,我们使用两次传入地址的方式,分别传入行列地址。
DRAM 的类型
- Synchronous DRAM (SDRAM)
- for addressing internal data to be transferred on each clock cycle
- beginning with the column address counts up to column address + burst size – 1 一次可以读出多个数据
 与 SRAM 配合形成 cache
与 SRAM 配合形成 cache
- Double Data Rate SDRAM (DDR SDRAM)
- Transfers data on both edges of the clock Provides a transfer rate of 2 data words per clock cycle